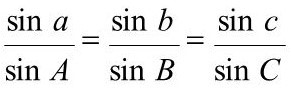TRIANGULATION
Triangulation is a surveying technique in which used to establish the required horizontal control for geodetic surveying in hilly and undulated areas. As we all known from simple geometry if all the three angles and the length of one of its sides of a triangle are known, then, the lengths of the remaining sides of the triangle can be calculated trigonometrically. Again, if the coordinates of any vertex of the triangle and azimuth of any side, are also known, then, the coordinates of the remaining vertices may be computed (Agor R, 1996). By extending this concept, in past surveyors tried to find the coordinates of unknown points using trigonometry. As an institute of awarding surveying science degrees to the students, in 2016 we were tried to establish a geodetic control network for Sabaragamuwa university premises using this method. This project was carried out by the surveying science students from the 2011/2012 batch with the cooperation of university academic and administrative staff. The entire project can be divided into the following steps for easy explanation.
- Preliminary investigation
- Office investigation
- Field investigation
- Organization of the program
- Field procedure
- Camping and erection of signals and towers
- Angle observation
- GPS observation
- Calculate coordinates of unknown trigonometric station using field observation and spherical trigonometric theories.
Preliminary investigation
Preliminary investigation is very important in triangulations. The accuracy, geometrical strength, simplicity, and economy of the triangulation scheme depend on the preliminary investigation and it helps to determine the best planning and management with optimum usage of available resources, achieving the required accuracy and reducing the cost. In triangulation it can be categorized in to two steps as office and field investigation.
Office investigation
Office investigation was conducted to select the best six trigonometric stations from the eight available stations to design the most suitable figure for the project. for this purpose, we used six indicators such as intervisibility between stations, possible ways to access the stations, formation of well-conditioned triangles. (angle more than 30° & less than 120°), the length of the sights (neither too small nor too large), convenience to supply meals to the trigonometric point and handiness to transfer GPS and precise theodolite. Then we then formed six groups, each with 14 members, and assigned every group to a specific trigonometric station. I was assigned to group 2, which is assigned to the new Paraviyangala trigonometric station
Field investigation
Next, a reconnaissance survey was conducted as a preliminary field survey. In this survey we used binoculars, mirror signals and smoke to conclude previous findings on station intervisibility. And we examined the terrain to be surveyed, and collected some miscellaneous information regarding, Transport facilities, availability of water resources, availability of labor and camping ground.
Organization of the program
The whole triangulation project was limited to a time frame of 14 days. So, the task had to be well prepared to avoid unnecessary delays and extra expenses also it supports to complete the project successfully with its every listed goals and deliverables. Since the areas we have selected are rural mountains, the villagers are accustomed to hunting with traps and deadfalls. So, we informed about our presence in the mountains to legal authorities in order to convey the information to villagers as a safety precaution and also as a legal responsibility. Due to the limited resources available, such as vehicles and surveying equipment, we had to prepare schedules to share the resources with other trigonometric stations. We also created a budget overview and a list of necessary equipment and foods.
Field procedure
This is the ultimate mechanism of triangulation. Mainly it is consisting of three sections as Arrangement of Camps and Signal Tower, GPS observations and Angle observation.
- Arrangement of Camps and Signal Tower
- The signal tower must be of sufficient height for clear visibility and sufficient space under the plate to set up the survey instruments and for the surveyor’s work
- It must be clearly visible from a distance against any background
- It should provide easy and accurate bisection for the telescope
- It must be able to be accurately centered on the trigonometric point
- Global positioning System (GPS) Observations
- Angle Observation
- Set up the instrument at the trig station with precise leveling and centering
- Set the instrument zero to the first observation point (Hawagala Trig Station) with the face on the left
- Aim the instrument's telescope towards the signal lamp of the next station and improve the vision and record the horizontal angle
- Aim the telescope consecutively at the next 3 stations counterclockwise and recorded three horizontal angles
- Move the telescope slightly to the left at the last station and continue measuring the horizontal angle clockwise again from the last station to the first station and record the angles
- When the telescope reaches its starting point, move the face of the instrument to the right and perform the same steps as for the left.
- Calculate coordinates of unknown trigonometric station using field observation and spherical trigonometric theories.
- Calculate mean observed angles and standard deviations
- Calculate the azimuth and the distance between two known trig stations
- Calculate azimuths of all other sides of the triangles
- Reduction of Observed directions and distances to ellipsoid
- Length of all sides using spherical sine formular
- Calculate the approximate latitudes and longitudes of all unknown stations using Gauss Mid Latitude formula.
- Using the approximate coordinates and the reverse of Mid latitude formula , calculate the approximate included angles and distances.
- Form the F-matrix ( Error matrix ) and B-matrix ( Jacobean Matrix ).
- Using mean latitude and longitude for the entire area,calculate the radius of the Meridian and Prime vertical
- Solve the differentials and residuals. If residuals are too large, do iterations
- Calculate the final corrected observed angles and coordinates of unknown stations
Our trigonometric station was located far from the university premises so, we had to stay inside
the forest for two weeks, so as the first task of our
field practice we prepared temporary camps inside the forest. The next task was to fix the signal
towers on the trigonometric stations. As all observations were directed at the gas lamp that was
held vertically above the trigonometric station, the configuration of the signal tower requires
high precision, so we used L-shaped iron bars for this.
In addition, when repairing the signal tower, we also pay attention to the facts below,
Triangulation was practiced at a time when GPS technology was not yet born. However, the GPS observations were made so that the results of the triangulation process could be compared, and the accuracy can be verified. For this, we use Trimble GPS instruments as a rover station and at the same time the GPS base station was positioned at the Hawagala trigonometric station as it is a 2nd order trigonometric point in the national triangulation system.
For the measurements of the angles, we used the method of reiteration
with eight zeros and there were two sets of observation for both faces (left and right face).
Instrument: Precise Theodolite with least count of 1 seconds and it can be used to measure
horizontal and vertical angles.
Reiteration method: In this method, the station signals are bisected successively, and a value
is obtained for each direction in each of the various observation rounds.
Number of Zeros: Use to eliminate errors due to inaccurate graduations of the horizontal wheel
of the surveying instruments and the main idea is to start measuring with different initial
values (if/ the measurements are based on eight zeros (i.e. 180/8=22.5, the gap between the
initial values must be 22.5 degrees) , in the first round, the measurements start with 0 and
the second round it starts with 22.5 and the third round with 45 and so on.)
Angular observations were involved following steps:
The calculation process consists of 11 steps, and all calculations were based on spherical trigonometry and geodetic calculations For more reliable and easier calculations, we used MATLAB software to code the calculation and you can find the codes here.
In angle observation, all included angles of the triangulation network figure were observed eight times so,a mean was calculated as the value to be used for the calculations and the STD was calculated to form the weight matrix for the angles (weight = 1 / STD).
Mean
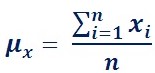
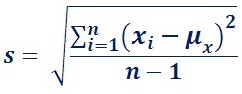
Next, the distance (This distance is referred to as the base distance of the network and is also measured precisely with the GPS) and azimuth of the first side of the triangulation network were calculated using the inverse mid latitude formula.
Coordinates of known points
| Station Name | Latitude | Longitude |
|---|---|---|
| Hawagala | 6˚43'8".06866 | 80˚44'42".38747 |
| Kirioluhena | 6˚37'16".66488 | 80˚49'58".27704 |
Then the azimuths of the other sides of triangles were calculated using a known azimuth and measured included angles. (These azimuths are called the approximate azimuths and are readjusted at the end of the calculation process)
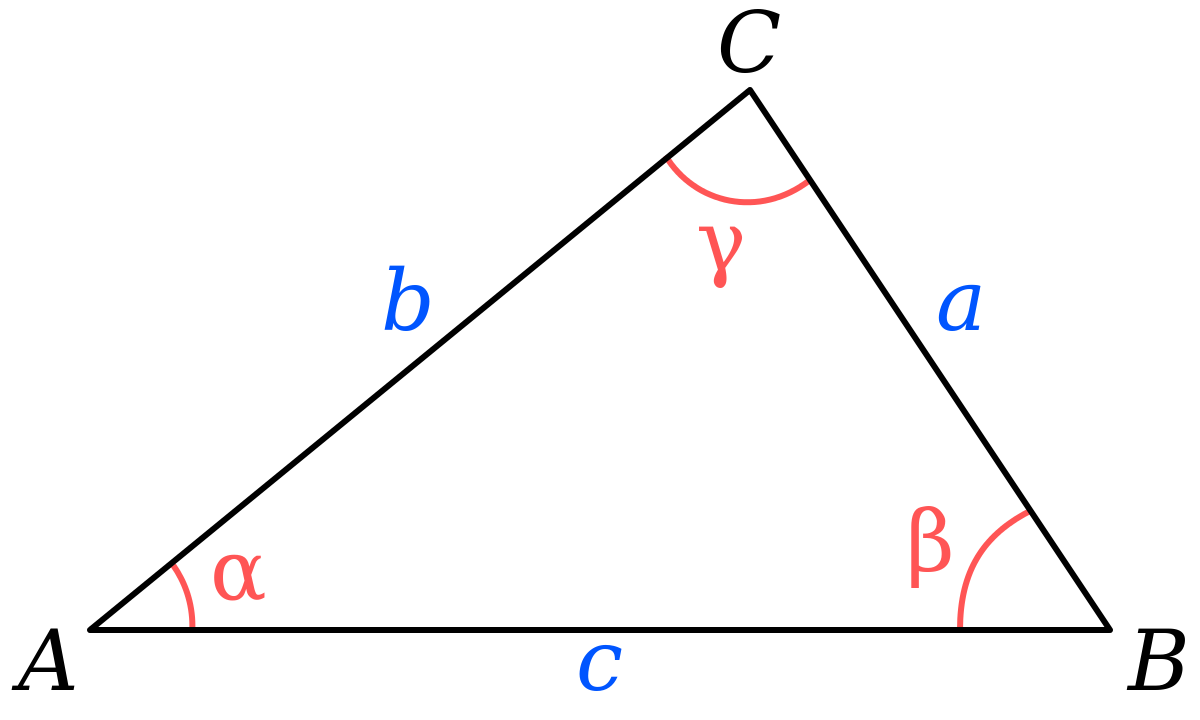
The horizontal angles observed in the field are planar angles and the calculations are based on the spherical angles. Therefore, measured normal directions were converted into the geodesic directions by applying appropriate corrections (δ1). At the same time, errors due to the height of the target (δ2) were also calculated and added to the measured values.
